🔢 NumPy Axes¶

The NumPy library in Python is a powerful tool for working with numerical data. Understanding how NumPy handles axes for vectors, matrices, and multidimensional arrays is key to efficiently manipulating data in these structures. Let's dive into it.

1. Understanding Axes in NumPy¶

An 'axis' in NumPy refers to a dimension of a multi-dimensional array. The axes are defined for arrays with more than one dimension (i.e., matrices, or arrays with 3 or more dimensions). A 2-dimensional array has two axes: the first running vertically downwards across rows (axis 0), and the second running horizontally across columns (axis 1).

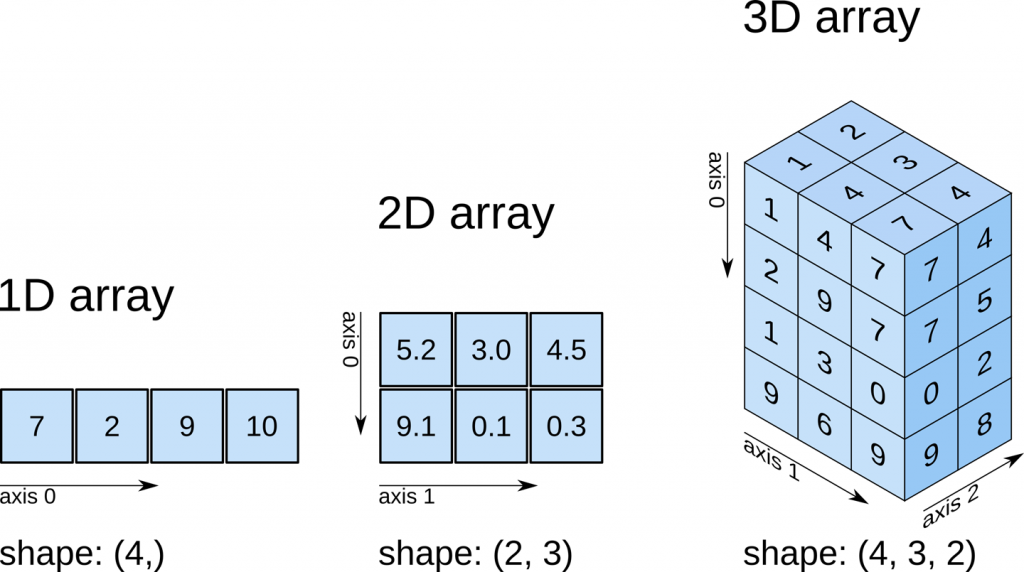
1.1 1-D Arrays (Vectors)¶

For 1-D arrays (vectors), there is only one axis (axis 0). The axis 0 is defined along the direction that increases the index of the elements.

In [9]:

import numpy as np

# 1-D array
arr = np.array([1, 2, 3, 4, 5])
print("Original array:\n", arr)
print("Shape of array: ", arr.shape, "\n")

# Operations along the axis
print("Sum: ", np.sum(arr, axis=0))
print("Min: ", np.min(arr, axis=0))
print("Max: ", np.max(arr, axis=0))
print("Mean: ", np.mean(arr, axis=0))

import numpy as np # 1-D array arr = np.array([1, 2, 3, 4, 5]) print("Original array:\n", arr) print("Shape of array: ", arr.shape, "\n") # Operations along the axis print("Sum: ", np.sum(arr, axis=0)) print("Min: ", np.min(arr, axis=0)) print("Max: ", np.max(arr, axis=0)) print("Mean: ", np.mean(arr, axis=0))

Original array:
 [1 2 3 4 5]
Shape of array:  (5,) 

Sum:  15
Min:  1
Max:  5
Mean:  3.0

1.2 2-D Arrays (Matrices)¶

For 2-D arrays (matrices), there are two axes: axis 0 runs vertically down the rows and axis 1 runs horizontally across the columns.

In [7]:

# 2-D array
arr = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
print("Original array:\n", arr)
print("Shape of array: ", arr.shape, "\n")

# Operations along axis 0
print("Sum along axis 0:\n", np.sum(arr, axis=0))
print("Min along axis 0:\n", np.min(arr, axis=0))
print("Max along axis 0:\n", np.max(arr, axis=0))
print("Mean along axis 0:\n", np.mean(arr, axis=0))

# Operations along axis 1
print("Sum along axis 1:\n", np.sum(arr, axis=1))
print("Min along axis 1:\n", np.min(arr, axis=1))
print("Max along axis 1:\n", np.max(arr, axis=1))
print("Mean along axis 1:\n", np.mean(arr, axis=1))

# 2-D array arr = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]]) print("Original array:\n", arr) print("Shape of array: ", arr.shape, "\n") # Operations along axis 0 print("Sum along axis 0:\n", np.sum(arr, axis=0)) print("Min along axis 0:\n", np.min(arr, axis=0)) print("Max along axis 0:\n", np.max(arr, axis=0)) print("Mean along axis 0:\n", np.mean(arr, axis=0)) # Operations along axis 1 print("Sum along axis 1:\n", np.sum(arr, axis=1)) print("Min along axis 1:\n", np.min(arr, axis=1)) print("Max along axis 1:\n", np.max(arr, axis=1)) print("Mean along axis 1:\n", np.mean(arr, axis=1))

Original array:
 [[1 2 3]
 [4 5 6]
 [7 8 9]]
Shape of array:  (3, 3) 

Sum along axis 0:
 [12 15 18]
Min along axis 0:
 [1 2 3]
Max along axis 0:
 [7 8 9]
Mean along axis 0:
 [4. 5. 6.]
Sum along axis 1:
 [ 6 15 24]
Min along axis 1:
 [1 4 7]
Max along axis 1:
 [3 6 9]
Mean along axis 1:
 [2. 5. 8.]

1.3 3-D Arrays¶

For 3-D arrays, there are three axes: axis 0 (depth), axis 1 (rows), and axis 2 (columns). Axis 0 is the depth dimension (think of each 2-D array in the 3-D array as a slice of depth), axis 1 is the vertical dimension, and axis 2 is the horizontal dimension.

In [10]:

# 3-D array
arr = np.array([[[1, 2, 3], [4, 5, 6]], [[7, 8, 9], [10, 11, 12]]])
print("Original array:\n", arr)
print("Shape of array: ", arr.shape, "\n")

# Operations along axis 0
print("Sum along axis 0:\n", np.sum(arr, axis=0))
print("Min along axis 0:\n", np.min(arr, axis=0))
print("Max along axis 0:\n", np.max(arr, axis=0))
print("Mean along axis 0:\n", np.mean(arr, axis=0))

# Operations along axis 1
print("Sum along axis 1:\n", np.sum(arr, axis=1))
print("Min along axis 1:\n", np.min(arr, axis=1))
print("Max along axis 1:\n", np.max(arr, axis=1))
print("Mean along axis 1:\n", np.mean(arr, axis=1))

# Operations along axis 2
print("Sum along axis 2:\n", np.sum(arr, axis=2))
print("Min along axis 2:\n", np.min(arr, axis=2))
print("Max along axis 2:\n", np.max(arr, axis=2))
print("Mean along axis 2:\n", np.mean(arr, axis=2))

# 3-D array arr = np.array([[[1, 2, 3], [4, 5, 6]], [[7, 8, 9], [10, 11, 12]]]) print("Original array:\n", arr) print("Shape of array: ", arr.shape, "\n") # Operations along axis 0 print("Sum along axis 0:\n", np.sum(arr, axis=0)) print("Min along axis 0:\n", np.min(arr, axis=0)) print("Max along axis 0:\n", np.max(arr, axis=0)) print("Mean along axis 0:\n", np.mean(arr, axis=0)) # Operations along axis 1 print("Sum along axis 1:\n", np.sum(arr, axis=1)) print("Min along axis 1:\n", np.min(arr, axis=1)) print("Max along axis 1:\n", np.max(arr, axis=1)) print("Mean along axis 1:\n", np.mean(arr, axis=1)) # Operations along axis 2 print("Sum along axis 2:\n", np.sum(arr, axis=2)) print("Min along axis 2:\n", np.min(arr, axis=2)) print("Max along axis 2:\n", np.max(arr, axis=2)) print("Mean along axis 2:\n", np.mean(arr, axis=2))

Original array:
 [[[ 1  2  3]
  [ 4  5  6]]

 [[ 7  8  9]
  [10 11 12]]]
Shape of array:  (2, 2, 3) 

Sum along axis 0:
 [[ 8 10 12]
 [14 16 18]]
Min along axis 0:
 [[1 2 3]
 [4 5 6]]
Max along axis 0:
 [[ 7  8  9]
 [10 11 12]]
Mean along axis 0:
 [[4. 5. 6.]
 [7. 8. 9.]]
Sum along axis 1:
 [[ 5  7  9]
 [17 19 21]]
Min along axis 1:
 [[1 2 3]
 [7 8 9]]
Max along axis 1:
 [[ 4  5  6]
 [10 11 12]]
Mean along axis 1:
 [[ 2.5  3.5  4.5]
 [ 8.5  9.5 10.5]]
Sum along axis 2:
 [[ 6 15]
 [24 33]]
Min along axis 2:
 [[ 1  4]
 [ 7 10]]
Max along axis 2:
 [[ 3  6]
 [ 9 12]]
Mean along axis 2:
 [[ 2.  5.]
 [ 8. 11.]]

By understanding axes in NumPy, you will be able to perform operations along any given dimension of an array. The axis parameter in various functions can be used to specify the dimension along which the operation is to be performed. This can be particularly useful when performing operations on multidimensional data, where you might want to perform calculations along a specific dimension, such as summing the values across rows or columns, finding max or min values, computing the mean, and more.